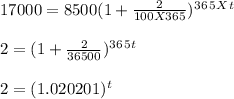(a)
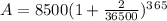
(b) A = $12680.37
(c)
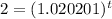
Step-by-step explanation:
Given:
Principal, P = $8,500
Rate of interest, r = 2%
Compounded continuously, n = 365
(a)
Time, t = 1
Amount, A equation = ?
We know:
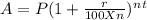
On substituting the value we get:
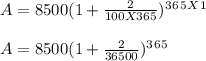
(b)
Amount after 20 years = ?
t = 20
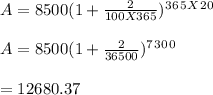
(c)
Amount to double = 8500 X 2
= $17000
Time, t = ?