Answer:
Therefore 53.05 mg will remain of the given radioactive substance after 35 hours.
Explanation:
Radioactive Decay:
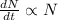
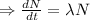
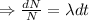
Integrating both sides
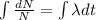
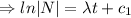
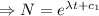
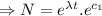
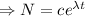 [
[
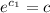 ]
]
When t=0,
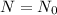 = initial amount
= initial amount
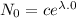

Therefore the decay equation is
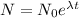
Given that,
 = Initial amount of the radioactive substance= 140 mg
= Initial amount of the radioactive substance= 140 mg
After 25 hours, 70 mg of substance remains.
N= 70 mg, t=25 hours
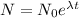
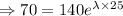
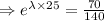
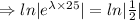
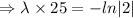 [
[
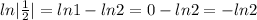 ]
]
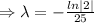
The decay equation becomes
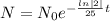
Now putting t= 35
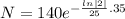
= 53.05 mg
Therefore 53.05 mg will remain of the given radioactive substance after 35 hours.