Question

Suppose that a certain radioactive element decays in such a way that every twenty years the mass of a sample of the element is one third of the initial mass. Given a 100 gram sample of the element, how much of the element remains after 17 years

Answer 1

Therefore 21.09 gram of the element remains after 17 years.

Explanation:

The decay rate is proportional to the number of nuclei.

`-(dN)/(dt)\propto N`

`\Rightarrow -(dN)/(dt)=\lambda N`

`\Rightarrow (dN)/(N)=-\lambda \ dt`

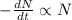
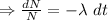
Integrating both sides

`\Rightarrow \int(dN)/(N)=\int-\lambda \ dt`

`\Rightarrow ln N= -\lambda t+C`

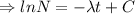
Initially N=
`N_0` , when t=0

`ln N_0= -\lambda .0+C`

`\Rightarrow C=ln \ N_0`

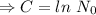
The equation becomes

`ln N=-\lambda t+ln N_0`

`\Rightarrow ln N-ln N_0=-\lambda t`

`\Rightarrow \ln(N)/(N_0)=-\lambda t`

`\Rightarrow N=N_0e^(-\lambda t)`

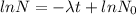
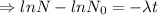
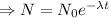
N= Remaining mass after t time

`N_0`= initial mass of the sample

`\lambda`= decay constant

Given that, every 12 years the mass of a sample of a the element is one third of the initial mass.

Here,
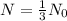`N=\frac13N_0`, t= 12 years

`\therefore \frac13N_0=N_0e^(-12\lambda )`

`\Rightarrow e^(-12\lambda )=\frac13`

`\Rightarrow ln e^(-12\lambda )=ln\frac13`

`\Rightarrow ln e^(-12\lambda )=ln1-ln3` [
`ln\frac ab = ln a- ln b` ]

`\Rightarrow {-12\lambda }= -ln 3` [
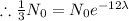
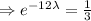
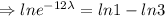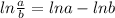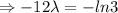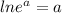`ln e^a=a` and
`ln 1=0`]

`\Rightarrow\lambda }=( ln 3)/(12)`

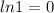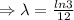
The equation becomes

`\therefore N=N_0e^{-(ln3)/(12) t}`

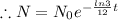
Given that, the initial amount
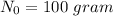`N_0= 100 \ gram` and t =17

`\therefore N=100e^{-(ln3)/(12) 17}`

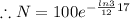
`\Rightarrow N=21.09` gram

Therefore 21.09 gram of the element remains after 17 years.