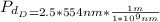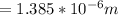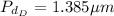Complete Question
In a Young's double-slit experiment, a set of parallel slits with a separation of 0.132 mm is illuminated by light having a wavelength of 554 nm and the interference pattern observed on a screen 4.50 m from the slits
(a) What is the difference in path lengths
from the two slits to the location of a third order bright fringe on the screen?
________ µm
(b) What is the difference in path lengths from the two slits to the location of the third dark fringe on the screen, away from the center of the pattern?
________ µm
Answer:
a
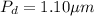
b
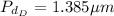
Step-by-step explanation:
Generally the path difference for a bright fringe is mathematically represented as
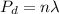
Where is n the order of fringe with values n = 0,1,23,4,...
 is the wavelength
is the wavelength
For n = 2 i.e for the third fringe
The path difference becomes
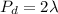
substituting values
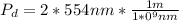

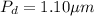
For dark fringe the formula is
![P_d__D} = [n+(1)/(2) ] \lambda](https://img.qammunity.org/2021/formulas/physics/college/tpvbp29kf56v37qorlrxnj6fmd02gnejy3.png)
Where n = 2 for third fringe