Question

Ti-6Al-4V has a fracture toughness of 74.6 MPa-m0.5. How much stress (in MPa) would it take to fail a plate loaded in tension that has a center-crack with a length of 10 mm (Assume plane strain conditions and f-1)? Would this stress change if the plate were made thinner? How? 0.5 20 Cl

Answer 1

critical stress = 595 MPa

Step-by-step explanation:

given data

fracture toughness = 74.6 MPa-
`√(m)`

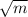
crack length = 10 mm

f = 1

solution

we know crack length = 10 mm

and crack length = 2a as given in figure attach

so 2a = 10

a = 5 mm

and now we get here with the help of plane strain condition , critical stress is express as

critical stress =
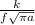`(k)/(f√(\pi a))` ......................1

put here value and we get

critical stress =
`\frac{74.6}{1\sqrt{\pi 5* 10^(-3)}}`

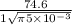
critical stress = 595 MPa

so here stress is change by plane strain condition because when plate become thinner than condition change by plane strain to plain stress.

plain stress condition occur in thin body where stress through thickness not vary by the thinner section.