Answer:
0.148 or 14.80%
Explanation:
Mean overhead reach (μ) = 200 cm
Standard deviation (σ) = 8.9 cm
The z-score for any reach, X, is given by:
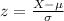
For a X = 209.30 cm:
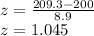
A z-score of 1.045 corresponds to the 85.20th percentile.
Therefore, the probability that an individual distance is greater than 209.30 cm is:
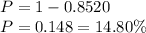
The probability is 0.148 or 14.80%