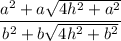Question

Two square pyramids are similar. If the ratio of a pair of corresponding edges is a : b, what is the ratio of their volumes? What is the ratio of their surface areas?

Answer 1

Ratio of their volumes = a³ : b³

Ratio of their surface areas =
`$\frac{a^(2) + a\sqrt{4h^(2)+a^(2)}}{b^(2) + b\sqrt{4h^(2)+b^(2)}}`

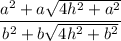
Explanation:

Two square pyramids are similar with their edges are in the ratio of a : b.

Volume of a square pyramid with edge and h = a is given by the formula,

=
`$(a^(2)* h )/(3)` =
`$(a^(3) )/(3)`

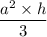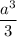
Volume of a square pyramid with edge b and h = b is given by the formula,

=
`$(b^(2)* h )/(3)` =
`$(b^(3) )/(3)`

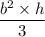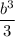
Ratio of their volumes = a³ : b³ since h/3 gets cancelled.

Total surface area of square pyramid with the edge a =

`$a^(2) + a\sqrt{4h^(2)+a^(2)}`

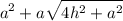
Total surface area of square pyramid with the edge b =

`$b^(2) + b\sqrt{4h^(2)+b^(2)}`

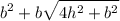
Ratio of the surface area =
`$\frac{a^(2) + a\sqrt{4h^(2)+a^(2)}}{b^(2) + b\sqrt{4h^(2)+b^(2)}}`