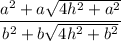Ratio of their volumes = a³ : b³
Ratio of their surface areas =
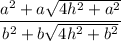
Explanation:
Two square pyramids are similar with their edges are in the ratio of a : b.
Volume of a square pyramid with edge and h = a is given by the formula,
=
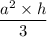 =
=
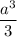
Volume of a square pyramid with edge b and h = b is given by the formula,
=
 =
=
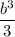
Ratio of their volumes = a³ : b³ since h/3 gets cancelled.
Total surface area of square pyramid with the edge a =
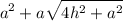
Total surface area of square pyramid with the edge b =
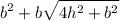
Ratio of the surface area =