Answer:
(a) 78.55Ω
(b) 720Ω
(c) 2181.8Ω
Step-by-step explanation:
(a) The inductive reactance,
 , is the opposition given to the flow of current through an inductor and it is given by;
, is the opposition given to the flow of current through an inductor and it is given by;
 = 2 π f L --------------------(i)
= 2 π f L --------------------(i)
Where;
f = frequency
L = inductance
From the question;
f = 50.0Hz
L = 250mH = 0.25H
Take π = 3.142 and substitute these values into equation (i) as follows;
 = 2 π (50.0) (0.25)
= 2 π (50.0) (0.25)
 = 25(3.142)
= 25(3.142)
 = 78.55Ω
= 78.55Ω
Therefore, the inductive reactance is 78.55Ω
(b) The capacitance reactance,
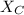 , is the opposition given to the flow of current through a capacitor and it is given by;
, is the opposition given to the flow of current through a capacitor and it is given by;
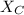 = (2 π f C) ⁻ ¹ --------------------(ii)
= (2 π f C) ⁻ ¹ --------------------(ii)
Where;
f = frequency
C = capacitance
From the question;
f = 50.0Hz
C = 4.40μF = 4.40 x 10⁻⁶ F
Take π = 3.142 and substitute these values into equation (ii) as follows;
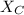 = [2 π (50.0) (4.40 x 10⁻⁶)] ⁻ ¹
= [2 π (50.0) (4.40 x 10⁻⁶)] ⁻ ¹
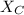 = [440 x (3.142) x 10⁻⁶)] ⁻ ¹
= [440 x (3.142) x 10⁻⁶)] ⁻ ¹
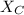 = [1382.48 x 10⁻⁶] ⁻ ¹
= [1382.48 x 10⁻⁶] ⁻ ¹
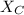 = [1.382 x 10⁻³] ⁻ ¹
= [1.382 x 10⁻³] ⁻ ¹
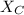 = 0.72 x 10³ Ω
= 0.72 x 10³ Ω
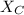 = 720Ω
= 720Ω
Therefore, the capacitive reactance is 720Ω
(c) Impedance, Z, is the ratio of maximum voltage,
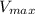 to maximum current,
to maximum current,
 , flowing through a circuit. i.e
, flowing through a circuit. i.e
Z =
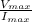 -------------------(iii)
-------------------(iii)
From the question;
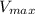 = 240V
= 240V
 = 110mA = 0.11A
= 110mA = 0.11A
Substitute these values into equation (iii) as follows;
Z =
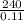
Z = 2181.8Ω
Therefore, the impedance in the circuit is 2181.8Ω