Question

Which is the correct way to solve the given equation

Answer 1

Option 2.
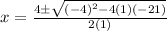`x = \frac{4 \pm \sqrt{(-4)^(2)-4 (1)(-21)}}{2 (1)}` shows the correct way to use the quadratic formula to solve the given equation.

Explanation:

Step 1:

For an equation of the form
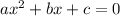`ax^(2) +bx+c=0` the solution is
`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`.

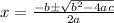Here a is the coefficient of
`x^(2)`, b is the coefficient of x and c is the constant term.

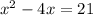`x^(2) -4x=21` can also be written as
`x^(2) -4x-21=0.`

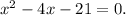
Comparing
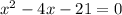`x^(2) -4x-21=0` with
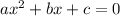`ax^(2) +bx+c=0`, we get that a is 1, b is -4 and c is -21.

To get the solution, we substitute the values of a, b, and c in
`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}`.

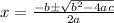Step 2:

Substituting the values, we get

`x=\frac{-b \pm \sqrt{b^(2)-4 a c}}{2 a}= \frac{-(-4) \pm \sqrt{(-4)^(2)-4 (1)(-21)}}{2 (1)}.`

`\frac{-(-4) \pm \sqrt{(-4)^(2)-4 (1)(-21)}}{2 (1)} = \frac{4 \pm \sqrt{(-4)^(2)-4 (1)(-21)}}{2 (1)}.`

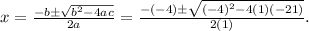
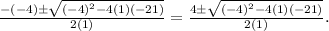
This is option 2.