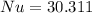Answer:
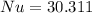
Step-by-step explanation:
Let consider that pipe is a horizontal cylinder. The Nusselt number is equal to:
![Nu = \left\{0.6+\frac{0.387\cdot Ra_(D)^{(1)/(6) }}{[1+\left((0.559)/(Pr) \right)^{(9)/(16)} ]^{(8)/(27) }} \right\}^(2)](https://img.qammunity.org/2021/formulas/physics/college/lxse7n1r79kmaf4tcgcmwdw1uzauji571t.png) , for
, for
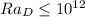 .
.
Where
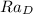 is the Rayleigh number associated with the cylinder.
is the Rayleigh number associated with the cylinder.
The Rayleigh number is:
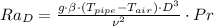
By assuming that air behaves ideally, the coefficient of volume expansion is:
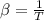
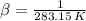
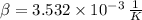
The cinematic and dynamic viscosities, thermal conductivity and isobaric specific heat of air at 10 °C and 1 atm are:
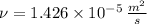
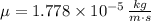
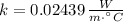
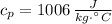
The Prandtl number is:
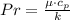
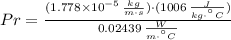
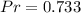
Likewise, the Rayleigh number is:
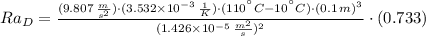
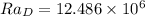
Finally, the Nusselt number is:
![Nu = \left\{0.6+\frac{0.387\cdot (12.486* 10^(6))^{(1)/(6) }}{\left[1 + \left((0.559)/(0.733)\right)^{(9)/(16) }\right]^{(8)/(27) }} \right\}^(2)](https://img.qammunity.org/2021/formulas/physics/college/ydy91234uk1zab486raos225oq5zxpg5no.png)