Question

Suppose Acap Corporation will pay a dividend of $2.73 per share at the end of this year and $3.06 per share next year. You expect Acap’s stock price to be $53.83 in two years. Assume that Acap’s equity cost of capital is 8.6%.

a. What price would you be willing to pay for a share of Acap stock today, if you planned to hold the stock for two years?
b. Suppose instead you plan to hold the stock for one year. For what price would you expect to be able to sell a share of Acap stock in one year?
c. Given your answer in (b), what price would you be willing to pay for a share of Acap stock today if you planned to hold the stock for one year? How does this compare to your answer in (a)?

Answer 1

Step-by-step explanation:

Year 1: Dividend, D1 = $2.73

Year 2: Dividend, D2 = $3.06

Year 2: Stock Price, P2 = $53.83

Cost of Capital, r = 8.6% = 0.086

(a.)

let Current Price = Po = D1/(1 + r)² + D2/(1 + r)² + P2/(1 + r)²

`P0 = (2.73)/(1.086^(2) ) + (3.06)/(1.086^(2) ) + (53.83)/(1.086^(2) )`

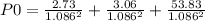
Current Price, Po = $50.75

(b.)

let Year 1 stock price = P1 = D2/(1 + r) + P2/(1 + r)

`P1 = (3.06)/(1.086) + (53.83)/(1.086)`

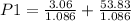
Stock Price Year 1, P1 = $52.38

(c.)

price am Willing to pay, Po = D1/(1 + r) + P1/(1 + r)

`P0 = (2.73)/(1.086) + (52.38)/(1.086)`

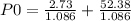
Current Price, P0 = $50.75

The part c is almost the same as part a answer

Answer 2

a. $50.75

b. $52.38

c.$50.75

The answer in part c compares to a in that it has the same exact value as what was obtained in part a

Step-by-step explanation:

In this question, we are asked to calculate some share prices for Acap corporation given the data in the question. We proceed as follows;

a) dividend next year, D1 = $2.73

dividend at the end of 2nd year, D2 = $3.06

expected price in 2 years, P2 = $53.83

cost of capital , r = 8.6%= 0.086

P0( price willing to pay today) = [D1/(1+r)] + [ D2/(1+r)^2 ] + [P2/(1+r)^2] = [2.73/(1.086)] + [ 3.06/(1.086)^2 ] + [53.83/(1.086)^2] = $50.75

b) expected selling price in 1 year =Price in year 1 = (D2+P2)/(1+r)^1= (3.06+53.83)/(1.086) = $52.38

c) if investment period is 1 year

Price willing to pay today , P0 = (D1+P1)/(1+r) = (2.73+52.38)/(1.086) = $50.75