Answer:
a) the amount of energy produced in kJ/K is 0.73145 kJ/K
b) the amount of energy produced in kJ/K is 0.68975 kJ/K
The value for entropy production obtained using constant specific heats is approximately 6% higher than the value obtained when accounting explicitly for the variation in specific heats.
Step-by-step explanation:
Draw the T-s diagram.
a)
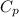 = 0.939 kJ/kg.K , m = 5 kg , T₂ = 520 K , T₁ = 280
= 0.939 kJ/kg.K , m = 5 kg , T₂ = 520 K , T₁ = 280
R = [8.314 kJ / 44.01 kg.K] , P₂ = 20 bar , P₁ = 2 bar
Δs =
![m[c_p ln((T_2)/(T_1)) - Rln((P_2)/(P_1))]](https://img.qammunity.org/2021/formulas/engineering/college/130oyemue6ebn3w2lbkm2m6wm9quyvfwor.png)
Substitute all parameters in the equation
Δs =
![5[(0.939) ln((520)/(280)) - ((8.314)/(44.01))ln((20)/(2))]](https://img.qammunity.org/2021/formulas/engineering/college/jmr0jv97cm3ikn38s0n1y6cuqv88zfx8z5.png)
Δs = 5 kg × 0.14629 kJ/kg.K
= 0.73145 kJ/K
b)
Δs =
![m[(s^0(T_2) - s^0(T_1))/(M) - Rln((P_2)/(P_1))]](https://img.qammunity.org/2021/formulas/engineering/college/gl3lgrju5nferv913jgr9q69dne19hh8jv.png)
Where T₁ = 280 K , s°(T₁) = 211.376 kJ/kmol.K
T₂ = 520 K , s°(T₂) = 236.575 kJ/kmol.K
R = [8.314 kJ / 44.01 kg.K] , M = 44.01 kg.K , P₂ = 20 bar , P₁ = 2 bar
Δs =
![5[(236.575 - 211.376)/(44.01) - ((8.314)/(44.01))ln((20)/(2))]](https://img.qammunity.org/2021/formulas/engineering/college/22mnz5wtg6952jvqnto34eabn0shyn368p.png)
= 5 kg (0.13795 kJ/kg.K)
= 0.68975 kJ/K
The value for entropy production obtained using constant specific heats is approximately 6% higher than the value obtained when accounting explicitly for the variation in specific heats.