Question

The diagram shows a right triangle and three squares. The area of the largest square is 67 units squared.

Which could be the areas of the smaller squares?
Choose all answers that apply:

(Choice A)
A
8 and 58
(Choice B)
7 and 60

(Choice C)

11 and 56
PS this is a Khan Academy question

Answer 1

B. 7 and 60

C. 11 and 56

Explanation:

see the attached figure to better understand the problem

we know that

The area of the three squares must satisfy the Pythagorean Theorem

so

`c^2=a^2+b^2`

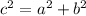
where

c^2 is the area of the largest square

a^2 and b^2 are the areas of the smaller squares

`67=a^2+b^2`

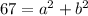
The sum of the areas of the smaller squares must be equal to 67

therefore

7 and 60 ----> could be the areas of the smaller squares (60+7=67)

11 and 56 ----> could be the areas of the smaller squares (11+56=67)