Answer:
B. 7 and 60
C. 11 and 56
Explanation:
see the attached figure to better understand the problem
we know that
The area of the three squares must satisfy the Pythagorean Theorem
so
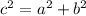
where
c^2 is the area of the largest square
a^2 and b^2 are the areas of the smaller squares
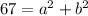
The sum of the areas of the smaller squares must be equal to 67
therefore
7 and 60 ----> could be the areas of the smaller squares (60+7=67)
11 and 56 ----> could be the areas of the smaller squares (11+56=67)