Answer:
V = 1.6777 m/s , 10.667 , 0 m/s
P = ( 20, 128, 0 ) kg-m/s
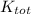 = 766 J
= 766 J
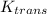 = 699.3 J
= 699.3 J
Krel = 66.7 J
Step-by-step explanation:
given data
Stiffness K = 460 N/m
Extension e = 0.37 m
solution
we know that here that center of mass is express as
V =
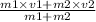 ................1
................1
V1 =
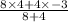
V1 = 1.6777 m/s
V2 =

V2 = 10.667 m/s
V3 =
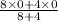
V3 = 0 m/s
and
P system is
P =
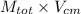
P = (8+4) × ( 1.6777 , 10.667 , 0 )
P = ( 20, 128, 0 ) kg-m/s
and
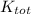 = K1 + K2
= K1 + K2
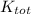 = 0.5 × m × v1² + 0.5 × m × v2²
= 0.5 × m × v1² + 0.5 × m × v2²
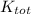 = 0.5 × 8 ×
= 0.5 × 8 ×
 + 0.5 × 4 ×
+ 0.5 × 4 ×
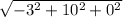
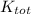 = 766 J
= 766 J
and
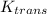 = 0.5 ×
= 0.5 ×
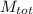 × ( V(cm)²)
× ( V(cm)²)
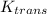 = 0.5 × (8+4) ×
= 0.5 × (8+4) ×
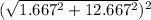
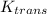 = 699.3 J
= 699.3 J
and
Krel =
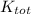 -
-
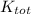
Krel = 766 J - 699.3 J
Krel = 66.7 J