Question

A projectile is thrown upward so that its distance above the ground after t seconds is h =-13t2 + 390t. After how many seconds does it reach its maximum height? A) 22.5 s B) 7 s C) 15 s D) 30 s

Answer 1

The option C) 15 s is correct

Therefore the maximum height it reaches in 15 seconds.

Explanation:

Given equation is
`h =-13t^2 + 390t`

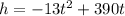
Given that a projectile is thrown upward so that its distance above the ground after t seconds is
`h =-13t^2 + 390t`

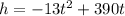
To find how many seconds does it reach its maximum height:

"The standard form of a parabola's equation is expressed as :

`y=ax^2+bx+c`.

If
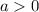`a>0`, then the parabola opens upwards;

if
`a<0` the parabola opens downwards."

The maximum height is the vertex of the parabola
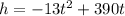`h =-13t^2 + 390t` which is
`(-b)/(2a)`.

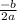Comparing the given equation with the standard form of parabola we get

the values of a=-13 , b=390 and c=0

The maximum height in
`t=(-b)/(2a)`.

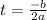Substitute the values we get

`t=-(390)/(2(-13))`

`=(390)/(26)`

`=15`

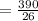
∴ t=15 s

∴ The option C) 15 s is correct.

∴ the maximum height is the vertex of the parabola, at t reaches in 15 seconds.