Question

2- A sheet of steel 3.0-mm thick has nitrogen atmospheres on both sides at 900°C and is permitted to achieve a steady-state diffusion condition. The diffusion coefficient for nitrogen in steel at this temperature is 1.85 à 10â10 m2/s, and the diffusion flux is found to be 1.0 à 10â7 kg/m2 . s. Also, it is known that the concentration of nitrogen in the steel at the high-pressure surface is 2 kg/m3. How far into the sheet from this high-pressure side will the concentration be 0.5 kg/m3? Assume a linear concentration profile. (40 pts.)

Answer 1

2.78x10⁻³ m

Step-by-step explanation:

Nitrogen diffusion in the steel can be expressed using the following equation:

`J = - D*(\Delta C)/(\Delta x) = - D*(C_(1) - C_(2))/(x_(1) - x_(2))`

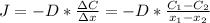
Where:

J: is the diffusion flux = 1.0x10⁻⁷ kgm⁻²s⁻¹

D: is the diffusion coefficient = 1.85x10⁻¹⁰ m²/s

C₁: is the concentration of nitrogen in the steel at the surface = 2 kg/m³

C₂: is the concentration of nitrogen at the distance x₂ = 0.5 kg/m³

x₁: is the distance at the surface = 0

x₂: is the distance to find

Hence, we have:

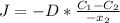`J = - D*(C_(1) - C_(2))/(- x_(2))` (1)

Solving equation (1) for x₂:

`x_(2) = D (C_(1) - C_(2))/(J) = 1.85 \cdot 10^(-10) m^(2)/s (2 kg/m^(3) - 0.5 kg/m^(3))/(1.0 \cdot 10^(-7) kgm^(-2)s^(-1)) = 2.78 \cdot 10^(-3) m`

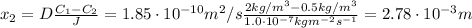
Therefore, the nitrogen will enter 2.78x10⁻³ m into the sheet.

I hope it helps you!