Question

Which function should be used to when evaluating the function at x = −5? HELP ASAP!!

Answer 1

Given:

Given that the function
`p(x)=\left\{\begin{array}{ll}(1)/(4) x^(2)+1 & \text { if } x \leq 3 \\(1)/(4) x+2.5 & \text { if } x>3\end{array}\right.`

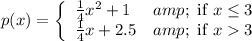
We need to determine the function to evaluate when x = -5.

Function:

The function is given two interval. The interval
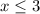`x\leq 3` means that x takes all values less than or equal to 3.

And the interval
`x>3` means that x takes all values greater than 3.

We need to determine the function that takes the limit when x = -5.

From the two limits, the limit x = -5 lie in the interval
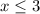`x\leq 3` because the interval takes all x values less than or equal to 3.

Hence, the function is
`p(x)=(1)/(4) x^(2)+1`

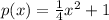
Thus, Option A is the correct answer.