Question

Which logarithmic equation has the same solution as x minus 4 = 2 cubed

log 3 squared = (x minus 4)
log 2 cubed = (x minus 4)
log Subscript 2 Baseline (x minus 4) = 3
log Subscript 3 Baseline (x minus 4) = 2

(look at the picture below)

Answer 1

The logarithmic equation that has the same solution as x - 4 = 2^3 is log2(x - 4) = 3.

Step-by-step explanation:

The logarithmic equation that has the same solution as x - 4 = 23 is log2(x - 4) = 3.

To explain this, we need to understand how logarithms and exponentiation are related. When an equation is written in exponential form, such as 23 = 8, we can rewrite it in logarithmic form as log2(8) = 3. In this case, we have x - 4 = 23, which means that 23 = (x - 4). Using the logarithmic property, we can rewrite this equation as log2(x - 4) = 3.

Answer 2

Given:

The given equation is
`x-4=2^(3)`

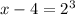
Solving the equation
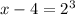`x-4=2^(3)`, we get;

`x-4=8`

`x=12`

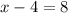
We need to determine the logarithmic equation that is equivalent to the given equation.

Option A:
`\log 3^(2)=(x-4)`

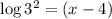
Simplifying, we get;

`\log 9=x-4`

`\log 9+4=x`

`4.95=x`

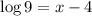
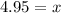
Since, the values of x are not equivalent, the equation
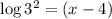`\log 3^(2)=(x-4)` is not equivalent to
`x-4=2^(3)`

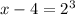
Option A is not the correct answer.

Option B:
`\log 2^(3)=x-4`

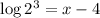
Simplifying, we get;

`\log 8=x-4`

`\log 8+4=x`

`4.9=x`

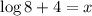
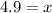
Since, the values of x are not equivalent, the equation
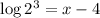`\log 2^(3)=x-4` is not equivalent to
`x-4=2^(3)`

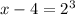
Option B is not the correct answer.

Option C:
`\log _(2)(x-4)=3`

Simplifying, we get;

`x-4=2^(3)`

`x-4=8`

`x=12`

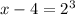
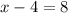
Since, the values of x are equivalent, the equation
`\log _(2)(x-4)=3` is equivalent to
`x-4=2^(3)`

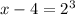
Hence, Option C is the correct answer.

Option D:
`\log _(3)(x-4)=2`

Simplifying, we get;

`x-4=3^2`

`x-4=9`

`x=13`

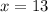
Since, the values of x are not equivalent, the equation
`\log _(3)(x-4)=2` is not equivalent to
`x-4=2^(3)`

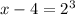
Hence, Option D is not the correct answer.