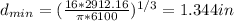Question

The driveshaft of an automobile is being designed to transmit 134 hp at 2900 rpm. Determine the minimum diameter d required for a solid steel shaft if the allowable shear stress in the shaft is not to exceed 6100 psi.

Answer 1

The minimum diameter is 1.344 in

Step-by-step explanation:

The angular speed of the driveshaft is equal to:

`w=(2\pi N)/(60)`

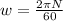
Where

N = rotational speed of the driveshaft = 2900 rpm

`w=(2\pi *2900)/(60) =303.69rad/s`

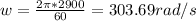
The torque in the driveshaft is equal to:

`\tau=(P)/(w)`

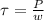
Where

P = power transmitted by the driveshaft = 134 hp = 73700 lb*ft/s

`\tau=(73700)/(303.69) =242.68lb*ft`

The minimum diameter is equal to:

`d_(min) =((16T)/(\pi *\tau ) )^(1/3)`

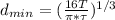
Where

T = shear stress = 6100 psi

τ = 242.68 lb*ft = 2912.16 lb*in

`d_(min) =((16*2912.16)/(\pi *6100) )^(1/3) =1.344in`