Question

A rigid copper tank, initially containing 1 m3 of air at 295 K, 5 bar, is connected by avalve to a large supply line carrying air at 295 K, 15 bar. The valve is opened only as long as required tofill the tank with air to a pressure of 15 ,bar at which point the air in the tank is at 310 .K The copper tank,which has a mass of 20 ,kg is at the same temperature as the air in the tank, both initially and finally. Thespecific heat of the copper is c=0.385 kJ/kg K. Assuming ideal gas behavior for the air, determine:

(a) the initial and final mass of the air within the tank, each in kg, and
(b) the heat transfer to the surroundings from the tank and its contents, in kJ, ignoring kinetic and potential energy effects.

Answer 1

Initial mass = 5.91 kg

Final mass = 16.8 kg

Heat transfer Q = - 625.9 KJ

Step-by-step explanation:

Given data

Tank volume V = 1
`m^(3)`

Entering outside air temperature
`T_(i) = 295 K`

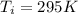
Entering outside air pressure
`P_(i)` = 15 bar

Initial tank pressure
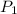`P_(1)` = 5 bar

Initial tank temperature
`T_(1)` = 295 K

Final pressure
`P_(2)` = 15 bar

Final temperature
`T_(2)` = 310 K

We know that

P V = m R T

(a). Initial mass is given by

`m_(1) = (P_(1) V_(1) )/(R T_(1) )`

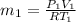
Put all the values in given equation

`m_(1) = ((500000)(1))/((287)(295)) = 5.91 \ kg`

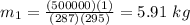
(b). Final mass is given by

`m_(2) = ((1500000)(1))/((287)(310))`

`m_(2) = 16.8 \ kg`

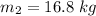
This is the final volume of the tank.

Δ U = Δ q +
`h_(i)` Δ
`m_(cv)`

`m_(2) u_(2) - m_(1) u_(1) = Q + h_(i) (m_(2) - m_(1) )`

Specific internal energy at initial temperature & pressure
`u_(1)` = 210.5
`(KJ)/(Kg)`

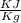
Specific internal energy at final temperature & pressure
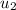`u_(2)` = 221.25
`(KJ)/(Kg)`

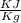
Specific enthalpy is
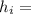`h_(i) =` 295.17
`(KJ)/(Kg)`

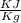
Q = ( 16.8 × 210.48 - 5.91 × 210.49 )- 295.17 ( 16.8 - 5.91 )

Q = 2292.23 - 3214.4

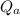`Q_(a)` = - 741.4 KJ

The heat transfer for the tank is given by

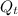`Q_(t)` = m C
`(T_(2) - T_(1))`

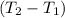
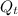`Q_(t)` = 20 × 0.385 × ( 310-295 )

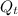`Q_(t)` = + 115.5 KJ

Total heat transfer Q =
`Q_(a)` +
`Q_(t)`

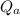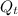
Q = - 741.4 + 115.5

Q = - 625.9 KJ

This is the heat transfer to the surrounding from the tank.