Question

Estimate the speed of the water free surface and the time required to fill with water a cone-shaped container 1.5 m high and 1.5m across at the top if the filling rate is 75.7 L/min.

Answer 1

speed of water is 0.0007138m/s

Step-by-step explanation:

From the law of conservation of mass

Rate of mass accumulation inside vessel = mass flow in - mass flow out

so, dm/dt = mass flow in - mass flow out

taking p as density

`d (dQ)/(dt) = pq_i_n`

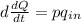
where,

q(in) is the volume flow rate coming in

Q = is the volume of liquid inside tank at any time

But,

dQ = Adh

where ,

A = area of liquid surface at time t

h = height from bottom at time t

A = πr²

r is the radius of liquid surface

`r = (1.5/2) / 1.5`
`h = (h)/(2)`

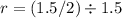
Hence,

`\pi( (h)/(2) )^2(dh)/(dt) =q_i_n`

`(dh)/(dt) = (q_i_n)/(\pi ((h)/(2))^2 ) =(4q_i_n)/(\pi h^2)`

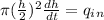
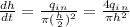
so, the speed of water surface at height h

`v = (dh)/(dt) =(4q_i_n)/(\pi h^2)`

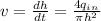
where,

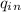`q_i_n` is 75.7 L/min = 0.0757m³/min

h = 1.5m

so,

`v = (4 * 0.0757)/(\pi * 1.5^2) \\\\v = 0.04283m/min`

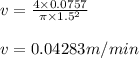
v = 0.04283 /60

v = 0.0007138m/s

Hence, speed of water is 0.0007138m/s