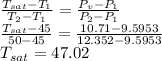Answer:
a) The air-fuel ratio is 37.83 kg air/kg fuel
b) The dew-point temperature is 47.02°C
Step-by-step explanation:
a) The combustion equation is equal to:
C₈H₁₈ + 2.5a(O₂ + 3.76N₂) = xCO₂ + yH₂O + 9.4aN₂ + 1.5aO₂
The mass balance for each elements is equal to:
C: 8 = x
H: 18 = 2y, y = 9
O: 5a = 2x + y + 3a, a = 12.5
C₈H₁₈ + 31.25(O₂ + 3.76N₂) = 8CO₂ + 9H₂O + 117.5N₂ + 18.75O₂
The air fuel ratio is equal to:
Taking the molar mass of octane = 114 kg/mol
molar mass of air = 29 kg/mol
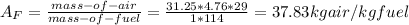
b) The dew-point temperature is:

Where Nv = moles of water vapor in products
Nprod = moles in the products
Pprod = total pressure = 1.8 atm = 182.38 kPa
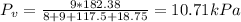
The saturation temperature at 10.71 kPa is obtained from saturated-water temperature tables and interpolation:
T₁ = 45°C
P₁ = 9.5953 kPa
T₂ = 50°C
P₂ = 12.352 kPa