Given:
M is the mid-point of RS
N is the mid-point of ST
MN = 18.4
To find:
The length of RT.
Solution:
The reference image is attached below.
Joining mid-point M and N, we get mid-segment MN.
MN is parallel to RT.
Triangle mid-segment theorem:
If a segments joins the mid point of a two sides of triangle, then the segment is parallel to the third side and is half of that side.
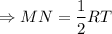
Substitute MN = 18.4
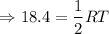
Multiply by 2 on both sides.
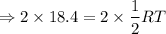
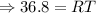
The length of RT is 36.8.