Question

Stefan sold 13 packages of cc and 1 package of cd for 147 dollars. Alberto sold 8 packages of wc and 10 packages of gb for 250 dollars. Find the cost each package of wc and one package of gb

Answer 1

The selling cost of 1 packet of w c = $ 10

The selling cost of 1 packet of g b = $ 17

Explanation:

Let us assume the cost of 1 packet of w c = $ m

and the cost of 1 packet of g b = $ n

The cost of 13 packages of w c + 1 package of g b = $ 147

⇒ 13 x ( cost of 1 package of w c ) + 1 package of g b = $ 147

⇒ 13 x (m) + 1 x (n) = 147

⇒13 m + n = 147 ..... (1)

The cost of 8 packages of w c + 10 package of g b = $ 250

⇒ 8 x ( cost of 1 package of w c ) + 10 x (cost of 1 package of g b ) = $ 250

⇒8 x (m) + 10 x (n) = 250

⇒ 8 m + 10 n = 250 ..... (2)

Now, solving for the values of m and n:

13 m + n = 147 ⇒ n = 147 - 13 m

Putting this in 8 m + 10 n = 250 , we get:

8 m + 10 ( 147 - 13 m) = 250

or, 8 m + 1470 - 130 m = 250

or, -122 m = -1220

or, m =
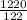`(1220)/(122)` = 10

⇒ m = $10

⇒ n = 147 - 13 (10) = 147 - 130 = 17 ⇒ n = $17

Hence, the cost of 1 packet of w c = $ 10

and the cost of 1 packet of g b = $ 17