Answer:
The comet might intersect the orbiting planet at (0, -4),
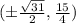 .
.
Explanation:
Given that, a planet follows an elliptical path described by
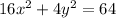 .........(1)
.........(1)
A comet follows the parabolic path
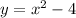
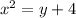 .........(2)
.........(2)
To find the intersecting point, we need to solve the above equations.
Putting
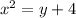 in the equation (1)
in the equation (1)
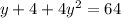
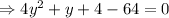
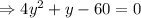

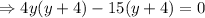
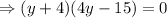
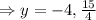
When y = -4 , then

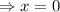
When
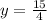 , then
, then
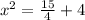
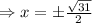
The comet might intersect the orbiting planet at (0, -4),
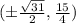 .
.