Question

A planet follows an elliptical path described by 16 x squared + 4 y squared = 64. A comet follows the parabolic path y equals x squared minus 4. Where might the comet intersect the orbiting​ planet?

Answer 1

The comet might intersect the orbiting planet at (0, -4),
`(\pm(√(31))/(2),(15)/(4))`.

Explanation:

Given that, a planet follows an elliptical path described by

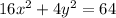`16x^2+4y^2=64` .........(1)

A comet follows the parabolic path

`y=x^2-4`

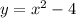
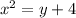`x^2=y+4`.........(2)

To find the intersecting point, we need to solve the above equations.

Putting
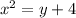`x^2=y+4` in the equation (1)

`y+4+4y^2=64`

`\Rightarrow 4y^2+y+4-64=0`

`\Rightarrow 4y^2+y-60=0`

`\Rightarrow 4y^2+16y-15y-60=0`

`\Rightarrow 4y(y+4)-15(y+4)=0`

`\Rightarrow(y+4)(4y-15)=0`

`\Rightarrow y=-4, (15)/(4)`

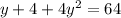
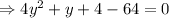
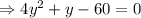
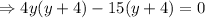
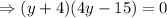
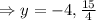
When y = -4 , then
`x^2=-4+4`
`\Rightarrow x=0`

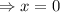
When
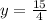`y=(15)/(4)`, then
`x^2=(15)/(4)+4`
`\Rightarrow x=\pm (√(31))/(2)`

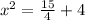
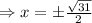
The comet might intersect the orbiting planet at (0, -4),
`(\pm(√(31))/(2),(15)/(4))`.