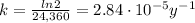Answer:
Explanation:
The decay rate of a radioactive isotope (also called activity of the isotope) is given by:
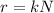
where
r is the decay rate
k is the decay constant
N is the number of nuclei in the radioactive sample
The decay constant of a radioactive isotope is also related to the half-life of the isotope by the formula
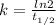
where
 is the half-life of the isotope, which is the time taken for the sample to halve, compared to its initial amount
is the half-life of the isotope, which is the time taken for the sample to halve, compared to its initial amount
In this problem, the half-life of plutioniun-239 is
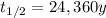
Therefore, the k-factor (decay constant) is: