2 Answers

Ignas · Answer 1 · 2021-02-14T02:48:25+0000

Answer:

Explanation:

The answer given below is not in the form you need. You need the form that includes radicals, not decimals. The formula for the half angle of sin is

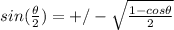$sin((\theta)/(2))=+/-\sqrt{(1-cos\theta)/(2) }$ so we need to find out what theta is. If our problem is

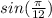$sin((\pi)/(12))$ , to get that into half angle form, it would be rewritten as

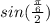$sin(((\pi)/(6) )/(2))$ so

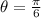
$\theta=(\pi)/(6)$

Look to your unit circle to find the EXACT VALUE of the cos of that angle.

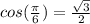
$cos((\pi)/(6))=(√(3) )/(2)$

Filling that into the formula for the half angle sin:

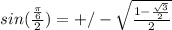$sin(((\pi)/(6) )/(2))=+/-\sqrt{(1-(√(3) )/(2) )/(2) }$ Doing a bit of simplifying gives you

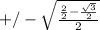$+/-\sqrt{((2)/(2) -(√(3) )/(2) )/(2) }$ and

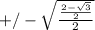$+/-\sqrt{((2-√(3) )/(2) )/(2) }$ and

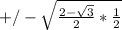$+/-\sqrt{(2-√(3) )/(2)* (1)/(2) }$ gives you

$+/-\sqrt{(2-√(3) )/(4) }$ which finally simplifies to

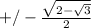
$+/-\frac{\sqrt{2-√(3) } }{2}$

That's the answer in exact format.

Please log in or register to add a comment.