Question

According to a study done by a university​ student, the probability a randomly selected individual will not cover his or her mouth when sneezing is 0.267. Suppose you sit on a bench in a mall and observe​ people's habits as they sneeze.

​(a) What is the probability that among 16 randomly observed individuals exactly 8 do not cover their mouth when​ sneezing?
​(b) What is the probability that among 16 randomly observed individuals fewer than 4 do not cover their mouth when​ sneezing?
​(c) Would you be surprised​ if, after observing 16 ​individuals, fewer than half covered their mouth when​ sneezing? Why?

Answer 1

a. P(X=8)=0.0277

b. P(X<4)=0.3460

c. No. P(X<8)=0.9605

Explanation:

a. Let x denote the event.

This is a binomial probability distribution problem expressed as

`P(X=x)={n\choose x}p^x(1-p)^(n-x)`

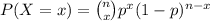
Where

• n is the total number of events
• p is the probability of a success
• x is the number of successful events.

Given that n=16, p=0.267, the probability of exactly 8 people not covering their mouths is calculated as:

`P(X=x)={n\choose x}p^x(1-p)^(n-x)\\\\\\P(X=8)={16\choose 8}0.267^8(1-0.267)^8\\\\\\=0.0277`

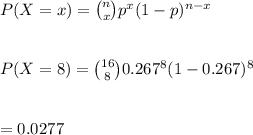
Hence, the probability of exactly 8 people not covering their mouths is 0.0277

b. The probability of fewer than 4 people covering their mouths is calculated as:

-We calculate and sum the probabilities of exactly 0 to exactly 3:

`P(X=x)={n\choose x}p^x(1-p)^(n-x)\\\\P(X<4)=P(X=0)+P(X=1)+P(X=2)+P(X=3)\\\\={16\choose 0}0.267^0(0.733)^(16)+{16\choose 1}0.267^0(0.733)^(15)+{16\choose 2}0.267^2(0.733)^(14)+{16\choose 3}0.267^3(0.733)^(13)\\\\=0.0069+0.0405+0.1106+0.1880\\\\=0.3460`

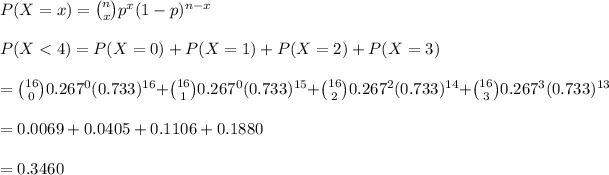
Hence, the probability of x<4 is 0.3460

c. Would you be surprised if fewer than half covered their mouths:

The probability of fewer than half covering their mouths is calculated as:

`P(X=x)={n\choose x}p^x(1-p)^(n-x)\\\\P(X<8)=P(X<4)+P(X=4)+P(X=5)+P(X=6)+P(X=7)\\\\=0.3460+{16\choose 4}0.267^4(0.733)^(12)+{16\choose 5}0.267^5(0.733)^(11)+{16\choose 6}0.267^6(0.733)^(10)+{16\choose 7}0.267^7(0.733)^(9)\\\\=0.3460+0.2225+0.1945+0.1299+0.0676\\\\=0.9605`

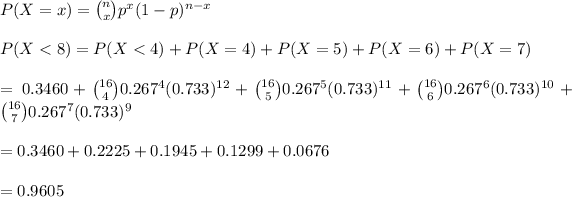
No. The probability of fewer than half is 0.9605 or 96.05%. This a particularly high probability that erases any chance of doubt or surprise.