Given:
The distance (in kilometers) Dora hiked is modeled as a function of time.
We need to determine the average rate of change in distance hiked, measured in kilometers per hour, between 8:30 am to 1:30 pm.
Average rate of change:
Let us write the time and the distance hiked in coordinates for the time 8:30 am and 1:30 pm.
Thus, the coordinates are (8.30, 4) and (1,12)
The average rate of change can be determined using the formula,

Substituting the points (8.30, 4) and (1.30,12), we get;
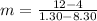


Rounding off to the nearest whole number, we get;
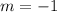
Therefore, the average rate of change is -1.