Question

In a recent​ poll, 44​% of survey respondents said​ that, if they only had one​ child, they would prefer the child to be a boy. Suppose you conducted a survey of 150 randomly selected students on your campus and find that 71 of them would prefer a boy.

​(a) Use the normal approximation to the binomial to approximate the probability​ that, in a random sample of 150 ​students, at least 71 would prefer a​ boy, assuming the true percentage is 44​%.
​(b) Does this result contradict the​ poll? Explain.

Answer 1

Step 1

Given, n= 150, p= 0.44, x=71.

The normal approximation of the binomial distribution can be used.

If np(1-p)
`\geq` 10 is satisfied:

np(1-p)= 150 x 0.44(1-0.44)=36.96 >10

Above rule is satisfied, thus we can use the normal approximation.

To find,

a. the probability​ that, in a random sample of 150 ​students, at least 71 would prefer a​ boy, assuming the true percentage is 44​%.

Step 2

Answer:

a. The Z - score is the value (using the continuity correction) decreased by the mean np and divided by the standard deviation

square root (np(1-p)

Z= x-np /
`√(np(1-p))`= 70.5 - (150 x0.44) /
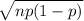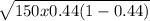`√(150 x 0.44(1-0.44))` = 0.7402

Determine the corresponding normal probability using the normal probability table is:

P(X
`\geq`71)=P(X> 70.5)= P( Z> 0.7402) =1 - P(Z< 0.7402)= 1-0.64396 =0.22919344

The probability that at least 71 students would prefer a boy is 0.22919344

Answer 2

a) The probability that 71 of 150 will prefer boy child is 71/150 or 0.47

b) The result contradicts the poll actual percentage is 47.33% which is 3.33% more than the poll predicted

Explanation:

If 71 out of 150 prefer boy child

The probability that the 71 will prefer boy child is

= 71/150

The actual percentage is

(71/150)*100%

= 47.33%

This contradicts the poll as this is more than the poll predicted. That means Less than 71 of 150 actually preferred boy child.