We can apply a translation (aka shifting) to angle 4 to slide it down until it matches up perfectly with angle 8. This is one way to see how the two angles are identical copies of each other.
Once we know that
 , we can then show that angles 5 and 8 are congruent by rotating angle 8 exactly 180 degrees around so that it lands perfectly on angle 5. By the transitive property we can say
, we can then show that angles 5 and 8 are congruent by rotating angle 8 exactly 180 degrees around so that it lands perfectly on angle 5. By the transitive property we can say
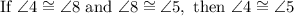
Another way is to reflect angle 4 over the transversal, and then slide it down so it matches up with angle 5. This bypasses the need for angle 8.
All of this is valid because of the parallel lines. If the lines weren't parallel, then angles 4 and 8 wouldn't be congruent (nor would angles 4 and 5). However, angles 5 and 8 are congruent since vertical angles are always congruent.