Question

Write an equation of a quadratic with roots of -1/4 and 3/2

Answer 1

Explanation:

First and foremost, a root is the same thing as a zero. It's called a zero because when x is equal to -1/4 (as it is here), y = 0. Where y = 0 is the x-axis. So if a quadratic has a 0 of -1/4, that is where the graph of the parabola goes through the x-axis.

If your quadratic has a zero of -1/4, that means that when y = 0, x = -1/4. Again, because this is a zero of the quadratic, then we can write it in factor form by setting x = -1/4 equal to 0. Do that like this:

If x = -1/4, then x + 1/4 = 0 and the factor is (x + 1/4) However, we do not want to leave that as a fraction. Take care of the fraction when it is set to equal 0:

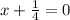`x+(1)/(4)=0` and multiply everything by 4:

`(4)x+(4)(1)/(4)x=(4)0` and simplify to

4x + 1 = 0 and the factor is

(4x + 1).

Do the same with the 3/2: If

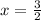`x=(3)/(2)`, then

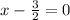`x-(3)/(2)=0`. Multiply everything by 2 to get:

`(2)x-(2)(3)/(2)=(2)0` to give you

2x - 3 = 0 and the factor is

(2x - 3).

FOIL those 2 factors together to get

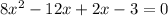`8x^2-12x+2x-3=0` which simplifies to

`8x^2-10x-3=0`

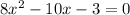
Now set it back equal to y and you're done!