Given:
b jointly varies with a and c. This can be written as,
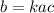
where k is a constant.
We need to determine the value of a when b = 72 and c = 2
Value of k:
Also, given that the value b = 112 when a = 12 and c = 7.
Hence, substituting these values in the expression
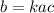 , we get;
, we get;
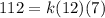
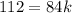
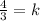
Thus, the value of k is
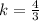
Value of a:
The value of a can be determined by substituting b = 72, c = 2 and
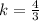 in the expression
in the expression
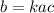 , we have;
, we have;
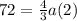
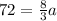
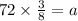
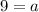
Therefore, the value of a is 9.