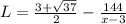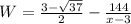Answer:
Required,
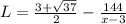
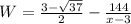
Explanation:
Given volume and depth respectively,
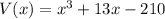 and
and
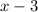
To find length and width of the rectanglular swiming pool we know,
Volume=length
 height
height
 depth.
depth.
Let depth=D=x-3, length=L, width=W, then
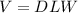
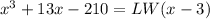
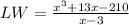
After divide we will get
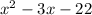 with remainder -144.
with remainder -144.
Thus,
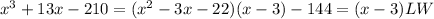
Now to find root of,
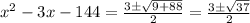
Thus,