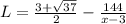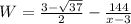Question

The volume of water and a rectangle swimming pool can be modeled by the function v(x)=x^3+13x-210. If the depth of the pool is given by the expression x-3, what are the expressions that represent the width and length of the pool?

Answer 1

Required,

`L=(3+√(37))/(2)-(144)/(x-3)`

`W=(3-√(37))/(2)-(144)/(x-3)`

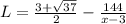
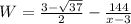
Explanation:

Given volume and depth respectively,

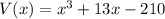`V(x)=x^3+13x-210` and
`x-3`

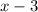
To find length and width of the rectanglular swiming pool we know,

Volume=length
`*`height
`*`depth.

Let depth=D=x-3, length=L, width=W, then

`V=DLW`

`x^3+13x-210= LW(x-3)`

`LW=(x^3+13x-210)/(x-3)`

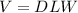
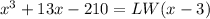
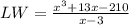
After divide we will get
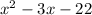`x^2-3x-22` with remainder -144.

Thus,

`x^3+13x-210=(x^2-3x-22)(x-3)-144=(x-3)LW`

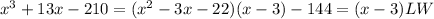
Now to find root of,

`x^2-3x-144=(3\pm√(9+88))/(2)=(3\pm √(37))/(2)`

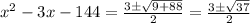
Thus,

`L=(3+√(37))/(2)-(144)/(x-3)`

`W=(3-√(37))/(2)-(144)/(x-3)`