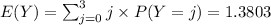Answer:
(a) 1.6197
(b) 1.3803
Explanation:
(a) Let X denote the number of games the Reds win. If Reds win exactly one it means that in the other two games Reds lost i.e Cubs won. Now, the probability of the Reds losing is determined by
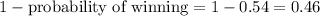 . So, if X wins exactly
. So, if X wins exactly
 times, then we should multiply the probabilities associated with
times, then we should multiply the probabilities associated with


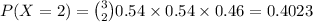
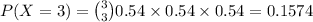
Now,
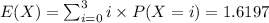
(b) Let Y denote the number of games won by Cubs. Then by the similar logic as above,
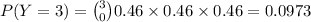
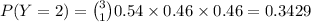
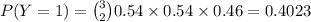
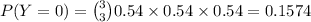
Now