Question

A 14kg Box rests on a frictionless surface. It is attached to a 8kg weight by a thin wire that passes over a frictionless pulley. The pulley is a uniform solid disk of mass 3kg and diameter 1m. After the box is released find (a) the tension in the wire on both sides of the pulley, (b) the acceleration of the box, and (c) the horizontal and vertical components of the force on the pulley

Answer 1

(a) Tension on both side of wire

`T_1=46.706 N`

`T_2=51.710 N`

(b) acceleration of the Box

`a = 3.336 (m)/(sec^2)`

(c) The horizontal and vertical components

Horizontal component
`T_1=46.706 N`

Vertical Component =130.19 N

Step-by-step explanation:

Refer attached figure for details.

`T_1\ \&\ T_2\ are\ tensions\ in\ the\ string\ and\ a\ is\ the\ acceleration\ of\ the\ masses.`

Applying Newton's 2 law of motion for 14 kg block in horizontal direction

`T_1 = 14\ a`-----------(i)

Similarly, applying Newton's 2 law of motion for 8 kg block in vertical direction

`8 g - T_2 =8 a`-----(ii)

Consider the case of pulley,

`\tau_e_x_t= I\alpha--------(iii)\\\\Where,\\\tau_e_x_t =Torque\ acting\ on\ the\ pulley\\I=moment\ of\ inertia\ of\ pulley\\\alpha= angular\ acceleration`

where,

`I= (MR^2)/(2) (for\ pulley\ disk)`

`I=(3\cdot0.5^2)/(2) =0.375\ kgm^2` (since mass of the pulley = 3 kg & Radius = 0.5 m)

&
`\tau_e_x_t= Net\ force \cdot Distance\ from\ application\ point`

Hence
`\tau_e_x_t = (T_2-T_1) \cdot (1)/(2) = 0.375\cdot\alpha`

`T_2-T_1=0.75\cdot\alpha`--------(iv)

Relation between linear acceleration (a) and angular acceleration (α) is as follows,

`a = R\alpha=0.5\cdot\alpha \ (R\ is \ radius\ of \ pulley)`

`\alpha=2a`--------------------(v)

Putting the value of (v) in to (iv)

`T_2 -T_1= 1.5 a`---------(vi)

adding equation (i),(ii) & (vi) gives

8g =22 a + 1.5 a

`a = 3.336 (m)/(sec^2)`

now putting the value of a in equation (i) & (ii) we get

`T_1=46.706 N`

`T_2=46.706 +1.5 \cdot 3.336` = 51.710 N

(a) Hence Tension on both side of wire

`T_1=46.706 N`

`T_2=51.710 N`

(b) acceleration of the Box

`a = 3.336 (m)/(sec^2)`

(c) The horizontal and vertical components

Horizontal component
`T_1=46.706 N`

Vertical Component =
`T_2+8\cdot g` =51.710 + 8 x 9.81 =130.19 N

Answer 2

Tension, T1 = 46.2 N and T2 = 52 N, where as acceleration = 3.3 ms^-2.

Forces on the pulley are 46.2 N , 81.4 N horizontal and vertical

respectively.

Step-by-step explanation:

Given:

Mass of the box on rest,
`m_1` = 14 kg

Mass of the attached box,
`m_2` = 8 kg

Mass of the pulley,
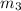`m_3` = 3 kg

Diameter of the pulley,
`d` = 1 m

Radius of the pulley,
`r` = 0.5 m

Here we will be using the concept of net force (
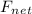`F_n_e_t`),net torque (
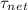`\tau_n_e_t`) and acceleration of the pulley .

A FBD is attached with.

Lets find the tension on the wire using Fnet.

⇒
`T_1=m_1(a)` ...for m1

⇒
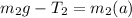`m_2g-T_2=m_2(a)` can be written as
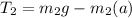`T_2=m_2g-m_2(a)` ...for m2

Considering clockwise torque as negative and anticlockwise torque as positive.

Moment of inertia (I) of the disk/pulley =
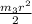`(m_3r^2)/(2)` and
`\alpha=(a)/(r)` .

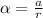Now using net torque on the pulley we can say that.

⇒
`(T_2-T_1)r=I\alpha`

⇒
`(T_2-T_1)r=(m_3r^2)/(2)* (a)/(r)`

⇒
`(T_2-T_1)=(m_3a)/(2)`

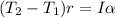
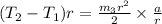
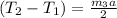
⇒ Plugging T1 and T2 .

⇒
`m_2g-m_2a-m_1a=(m_3a)/(2)`

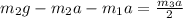
⇒ Isolating a from the rest.

⇒
`m_2g=(m_3a)/(2)+m_2a+m_1a`

⇒
`m_2g=a\ [(m_3)/(2)+m_2+m_1]`

⇒
`(m_2g)/((m_3)/(2) +m_2+m_1) =a`

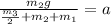
⇒ Plugging the numeric value

⇒
`((8* 9.8))/(((3)/(2) +8+14)) =a`

⇒
`3.3 =a`

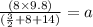
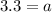
⇒ Acceleration = 3.3
`ms^-^2`

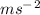
So,

(a).

Tension in the wire

⇒
`T_1=m_1(a)=14* 3.3 =46.2\ N`

⇒
`T_2=m_2g-m_2(a)=8(9.8-3.3)=52\ N`

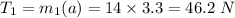
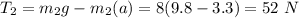
(b).

The acceleration of the box is 3.3 ms^-2.

(c).

Forces on the pulley.

Horizontal force,
`P_H` =
`T_1` =
`46.2\ N`

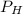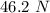
Vertical force,
`P_V` =
`T_2+m_3g` =
`52+3(9.8)` =
`81.4\ N`

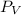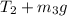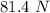
The values are as follows:

Tension as T1 = 46.2 N and T2 = 52 N ,where as acceleration =3.3 ms^-2.

Forces on the pulley are 46.2 N , 81.4 N horizontal and vertical

respectively.