Question

A 90 kg ice skater moving at 12.0 m/s on the ice encounters a region of roughed up ice with a coefficient of kinetic friction of 0.390.

How far along the rough ice does she go before stopping?

Answer 1

18.84m

Step-by-step explanation:

We are given;

Mass; m = 90 Kg

Initial velocity; u = 12 m/s

Coefficient of friction; μ = 0.390

Let,the combined mass of the ice skater and the skate be M

Thus, So,if the coefficient of frictional force is μ,then frictional force acting is; μN. N= Mg. Thus F_friction = μMg

Now, the deceleration due to friction will be, F_friction/M

Thus, deceleration = μMg/M

M will cancel out and we have; μg

Now, deceleration means negative acceleration. Thus acceleration (a) =

-μg

Now, to find the distance, let's use equation of motion which is;

v² = u² + 2as

Putting -μg for a, we have;

v² = u² + 2(-μg)s

v² = u² — 2μgs

We want to know the distance covered before coming to rest. Thus, v = 0m/s

So,

0² = 12² - (2 x 0.39 x 9.8 x s)

0 = 144 - 7.644s

Thus,

7.644s = 144

Thus, s = 144/7.644 = 18.84m

Answer 2

18.8m

Step-by-step explanation:

Let the distance traveled before stopping be 'd' m.

Given:

Mass of the skater (m) = 90 kg

Initial velocity of the skater (u) = 12.0 m/s

Final velocity of the skater (v) = 0 m/s (Stops finally)

Coefficient of kinetic friction (μ) = 0.390

Acceleration due to gravity (g) = 9.8 m/s²

Now, we know from work-energy theorem, that the work done by the net force on a body is equal to the change in its kinetic energy.

Hence, the net force acting on the skater is only frictional force which acts in the direction opposite to motion.

Frictional force is given as:

`f=\mu N`

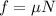
Where, 'N' is the normal force acting on the skater. As there is no vertical motion, N=mg

`f=\mu mg\\=0.390* 90* 9.8\\=343.98\ N`

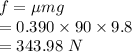
work done by friction is a negative work as friction and displacement are in opposite direction and is given as

`W=-fd=-343.98d`

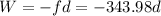
Now, change in kinetic energy is given as:

`\Delta K=(1)/(2)m(v^2-u^2)\\\\\Delta K=(1)/(2)* 90(0-12^2)\\\\\Delta K=45* (-144)=-6480\ J`

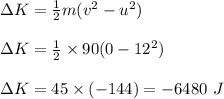
Therefore, from work-energy theorem,

`W=\Delta K\\\\-343.98d=6480\\\\d=(6480)/(343.98)\\\\d=18.8m`

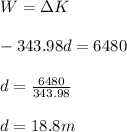
Hence, the skater covers a distance of 18.8 m before stopping.