Answer:
The initial angular acceleration of the beam is
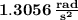
The magnitude of the force at A is 832.56N
Step-by-step explanation:
Here, m is the mass of the beam and l is the length of the beam.
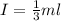
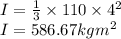
Take the moment about point A by applying moment equilibrium equation.
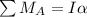
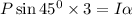
Here, P is the force applied to the attached cable and
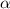 is the angular acceleration.
is the angular acceleration.
Substitute 350 for P and 586.67kg.m² for I
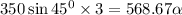
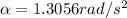
The initial angular acceleration of the beam is
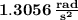
Find the acceleration along x direction

Here, r is the distance from center of mass of the beam to the pin joint A.
Substitute 2 m for r and 1.3056rad/s² for
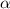
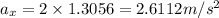
Find the acceleration along the y direction.
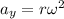
Here, ω is angular velocity.
Since beam is initially at rest,ω=0
Substitute 0 for ω
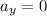
Apply force equilibrium equation along the horizontal direction.
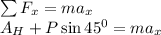
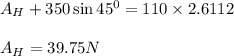
Apply force equilibrium equation along the vertical direction.
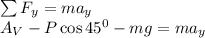
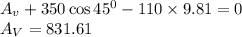
Calculate the resultant force,
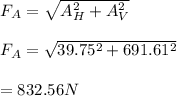
The magnitude of the force at A is 832.56N