Question

he uniform 110-kg beam is freely hinged about its upper end A and is initially at rest in the vertical position withθ= 0. Determine the initial angular accelerationα of the beam and the magnitudeFAof the force supported by the pin at A due to the application of the force P = 350 N on the attached cab

Answer 1

The initial angular acceleration of the beam is
`{\bf{1}}{\bf{.3056}}\,\frac{{{\bf{rad}}}}{{{{\bf{s}}^{\bf{2}}}}}`

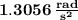
The magnitude of the force at A is 832.56N

Step-by-step explanation:

Here, m is the mass of the beam and l is the length of the beam.

`I =(1)/(3) ml`

`I=(1)/(3) *110*4^2\\I=586.67kgm^2`

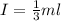
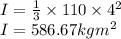
Take the moment about point A by applying moment equilibrium equation.

`\sum M_A =I \alpha`

`P \sin45^0 * 3 =I \alpha`

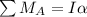
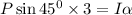
Here, P is the force applied to the attached cable and
`\alpha` is the angular acceleration.

Substitute 350 for P and 586.67kg.m² for I

`350 \sin 45^0 *3=568.67 \alpha`

`\alpha =1.3056rad/s^2`

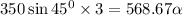
The initial angular acceleration of the beam is
`{\bf{1}}{\bf{.3056}}\,\frac{{{\bf{rad}}}}{{{{\bf{s}}^{\bf{2}}}}}`

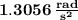
Find the acceleration along x direction

`a_x = r \alpha`

Here, r is the distance from center of mass of the beam to the pin joint A.

Substitute 2 m for r and 1.3056rad/s² for
`\alpha`

`a_x = 2* 1.3056 = 2.6112m/s^2`

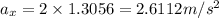
Find the acceleration along the y direction.

`a_y = r \omega ^2`

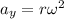
Here, ω is angular velocity.

Since beam is initially at rest,ω=0

Substitute 0 for ω

`a_y = 0`

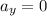
Apply force equilibrium equation along the horizontal direction.

`\sum F_x =ma_x\\A_H+P \sin45^0=ma_x`

`A_H + 350 \sin45^0=110*2.6112\\\\A_H=39.75N`

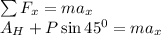
Apply force equilibrium equation along the vertical direction.

`\sum F_y =ma_y\\A_V-P \cos45^0-mg=ma_y`

`A_v +350 \cos45^0-110*9.81=0\\A_V = 831.61\\`

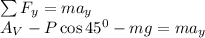
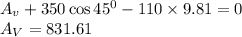
Calculate the resultant force,

`F_A=√(A_H^2+A_V^2) \\\\F_A=√(39.75^2+691.61^2) \\\\= 832.56N`

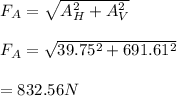
The magnitude of the force at A is 832.56N

Answer 2

a) Initial angular acceleration of the beam = 1.27 rad/s²

b)
`F_(A) = 851.11 N`

Step-by-step explanation:

`tan \theta = (opposite)/(Hypothenuse) \\tan \theta = (3)/(3) = 1\\\theta = tan^(-1) 1 = 45^(0)`

Force applied to the attached cable, P = 350 N

Mass of the beam, m = 110-kg

Mass moment of the inertia of the beam about point A =
`I_(A)`

Using the parallel axis theorem

`I_(A) = I_(G) + m((l)/(2) )^(2) \\I_(G) = (ml^(2) )/(12) \\I_(A) = (ml^(2) )/(12) + (ml^(2) )/(4) \\I_(A) = (ml^(2) )/(3)`

Moment = Force * Perpendicular distance

`\sum m_(A) = I_(A) \alpha\\`

From the free body diagram drawn

`\sum m_(A) = 3 Psin \theta\\ 3 Psin \theta = (ml^(2) \alpha )/(3)`

P = 350 N, l = 3+ 1 = 4 m, θ = 45°

Substitute these values into the equation above

`3 * 350 * sin 45 = (110 * 4^(2)* \alpha )/(3) \\\alpha = 1.27 rad/s^(2)`

Linear acceleration along the x direction is given by the formula

`a_(x) = r \alpha`

r = 2 m

`a_(x) = 2 * 1.27\\a_(x) = 2.54 m/s^(2)`

the linear acceleration along the y-direction is given by the formula

`a_(y) = r w^(2)`

Since the beam is initially at rest, w = 0

`a_(y) = 0 m/s^(2)`

General equation of motion along x - direction

`F_(x) + Psin \theta = ma_(x)`

`F_(x) + 350sin45 = 110 * 2.54\\F_(x) = 31.913 N`

General equation of motion along y - direction

`F_(x) + Pcos \theta - mg = ma_(y)`

`F_(y) + 350cos45 - 110*9.8 = m* 0\\F_(y) = 830.513 N`

Magnitude
`F_(A)` of the force supported by the pin at A

`F_(A) = \sqrt{F_(x) ^(2) + F_(y) ^(2) } \\F_(A) = \sqrt{31.913 ^(2) + 850.513 ^(2) } \\F_(A) = 851.11 N`