Question

A student team is to design a human powered submarine for a design competition. The overall length of the prototype submarine is 2.24 m, and its student designers hope that it can travel fully submerged through water at 0.560 m/s. The water is freshwater (a lake) at T = 15°C. The design team builds a one-eighth scale model to test in their university’s wind tunnel. A shield surrounds the drag balance strut so that the aerodynamic drag of the strut itself does not influence the measured drag. The air in the wind tunnel is at 25°C and at one standard atmosphere pressure. At what air speed do they need to run the wind tunnel in order to achieve similarity?

The students from the previous problem measure the aerodynamic drag on their model submarine in the wind tunnel. They are careful to run the wind tunnel at conditions that ensure similarity with the prototype submarine. Their measured drag force is 2.3 N. Estimate the drag force on the prototype submarine at the conditions given in Problem #3

Answer 1

1. The air speed at which wind tunnel should be ran in order to achieve similarity = 61.423 m/s

2. The drag force on the prototype submarine at the conditions given above = 10.325 N.

Step-by-step explanation:

1. Here we have

Density of water at 15 °C = 999.1 kg/m³

Density of air at 25 °C = 1.184 kg/m³

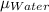`\mu_(Water)` at 15 °C = 1.138 × 10⁻³ kg/(m·s)

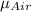`\mu_(Air)` at 25 °C = 1.849 × 10⁻⁵ kg/(m·s)

The formula is

`(V_m* \rho_m * L_m)/(\mu_m) = (V_p* \rho_p * L_p)/(\mu_p)`

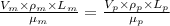
Where:

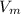`V_m` = Velocity of the model =

`\rho_m` = Density of the model medium at the medium temperature = 1.184 kg/m³

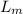`L_m` = Length of the model = 1/8 ×
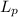`L_p` = 0.28 m

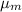`\mu_m` = Dynamic viscosity of model medium at the model medium temperature = 1.849 × 10⁻⁵ kg/(m·s)

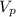`V_p` = Velocity of the prototype = 0.560 m/s

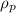`\rho_p` = Density of the prototype medium at the medium temperature = 999.1 kg/m³

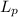`L_p` = Length of the prototype = 2.24 m

`\mu_p` = Dynamic viscosity of prototype medium at the prototype medium temperature 1.138 × 10⁻³ kg/(m·s)

Therefore

`{V_m}{} = (V_p* \rho_p * L_p * \mu_m)/(\mu_p* \rho_m * L_m)`

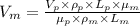
`{V_m}{} = (0.560* 999.1 * 2.24 * 1.849 * 10^(-5))/(1.138 * 10^(-3)* 1.184 * 0.28)` = 61.423 m/s

The air speed at which wind tunnel should be ran in order to achieve similarity = 61.423 m/s

2. The drag force on the prototype is given by

`F_(D.p) = F_(D.m)((\rho_p)/(\rho_m) )( (V_p)/(V_m))^2 ( (L_p)/(L_m))^2\\`

Where:

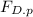`F_(D.p)` = Drag force of the prototype

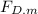`F_(D.m)` = Drag force of the model

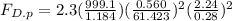`F_(D.p) =2.3((999.1 )/(1.184) )( (0.560 )/(61.423 ))^2 ( (2.24 )/(0.28))^2\\` = 10.325 N

The drag force on the prototype submarine at the conditions given above = 10.325 N.

Answer 2

a) The speed is 61.42 m/s

b) The drag force is 10.32 N

Step-by-step explanation:

a) The Reynold´s number for the model and prototype is:

`Re_(m) =(p_(m)V_(m)L_(m) )/(u_(m) )`

`Re_(p) =(p_(p)V_(p)L_(p) )/(u_(p) )`

Equaling both Reynold's number:

`(p_(p)V_(p)L_(p) )/(u_(p) )=(p_(m)V_(m)L_(m) )/(u_(m) )`

Clearing Vm:

`V_(m) =(p_(p)V_(p)L_(p) u_(m) )/(u_(p) p_(m) L_(m) )=(999.1*0.56*8*1.849x10^(-5) )/(1.138x10^(-3)*1.184*1 ) =61.42m/s`

b) The drag force is:

`(F_(Dm) )/(p_(m)V_(m)^(2)L_(m)^(2) ) =(F_(Dp) )/(p_(p)V_(p)^(2)L_(p)^(2) ) \\F_(Dp) =(F_(Dp)p_(p)V_(p)^(2)L_(p)^(2) )/(p_(m)V_(m)^(2)L_(m)^(2) ) \\F_(Dp)=(2.3*999.1*0.56^(2) *8^(2) )/(1.184*61.42^(2)*1^(2) ) =10.32N`