Question

A magnetic dipole with a dipole moment of magnitude 0.0243 J/T is released from rest in a uniform magnetic field of magnitude 57.5 mT. The rotation of the dipole due to the magnetic force on it is unimpeded. When the dipole rotates through the orientation where its dipole moment is aligned with the magnetic field, its kinetic energy is 0.458 mJ. (a) What is the initial angle between the dipole moment and the magnetic field

Answer 1

The initial angle between the dipole moment and the magnetic field is 47.76⁰

Step-by-step explanation:

Given;

magnitude of dipole moment, μ = 0.0243 J/T

magnitude of magnetic field, B = 57.5 mT

change in kinetic energy, ΔKE = 0.458 mJ

ΔKE = - ΔU

ΔKE = - (U₂ -U₁)

ΔKE = U₁ - U₂

U₁ -U₂ = 0.458 mJ

`(-\mu Bcos \theta_i )- (-\mu Bcos \theta_f) = 0.458 mJ\\\\-\mu Bcos \theta_i + \mu Bcos \theta_f = 0.458 mJ\\\\\mu Bcos \theta_f -\mu Bcos \theta_i = 0.458 mJ\\\\\mu B(cos \theta_f - cos \theta_i ) = 0.458 mJ`

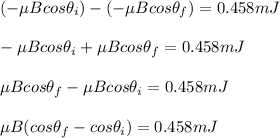
where;

θ₁ is the initial angle between the dipole moment and the magnetic field

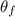`\theta_f` is the final angle which is zero (0) since the dipole moment is aligned with the magnetic field

μB(cos0 - cosθ₁) = 0.458 mJ

Substitute the given values of μ and B

0.0243 x 0.0575 (1 - cosθ₁) = 0.000458

0.00139725 (1 - cosθ₁) = 0.000458

(1 - cosθ₁) = 0.000458 / 0.00139725

(1 - cosθ₁) = 0.327787

cosθ₁ = 1 - 0.327787

cosθ₁ = 0.672213

θ₁ = cos⁻¹ (0.672213)

θ₁ = 47.76⁰

Thus, the initial angle between the dipole moment and the magnetic field is 47.76⁰

Answer 2

47.76°

Step-by-step explanation:

Magnitude of dipole moment = 0.0243J/T

Magnetic Field = 57.5mT

kinetic energy = 0.458mJ

∇U = -∇K

Uf - Ui = -0.458mJ

Ui - Uf = 0.458mJ

(-μBcosθi) - (-μBcosθf) = 0.458mJ

rearranging the equation,

(μBcosθf) - (μBcosθi) = 0.458mJ

μB * (cosθf - cosθi) = 0.458mJ

θf is at 0° because the dipole moment is aligned with the magnetic field.

μB * (cos 0 - cos θi) = 0.458mJ

but cos 0 = 1

(0.0243 * 0.0575) (1 - cos θi) = 0.458*10⁻³

1 - cos θi = 0.458*10⁻³ / 1.397*10⁻³

1 - cos θi = 0.3278

collect like terms

cosθi = 0.6722

θ = cos⁻ 0.6722

θ = 47.76°