Answer:
The initial angle between the dipole moment and the magnetic field is 47.76⁰
Step-by-step explanation:
Given;
magnitude of dipole moment, μ = 0.0243 J/T
magnitude of magnetic field, B = 57.5 mT
change in kinetic energy, ΔKE = 0.458 mJ
ΔKE = - ΔU
ΔKE = - (U₂ -U₁)
ΔKE = U₁ - U₂
U₁ -U₂ = 0.458 mJ
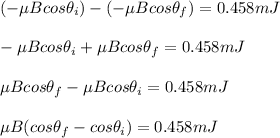
where;
θ₁ is the initial angle between the dipole moment and the magnetic field
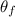 is the final angle which is zero (0) since the dipole moment is aligned with the magnetic field
is the final angle which is zero (0) since the dipole moment is aligned with the magnetic field
μB(cos0 - cosθ₁) = 0.458 mJ
Substitute the given values of μ and B
0.0243 x 0.0575 (1 - cosθ₁) = 0.000458
0.00139725 (1 - cosθ₁) = 0.000458
(1 - cosθ₁) = 0.000458 / 0.00139725
(1 - cosθ₁) = 0.327787
cosθ₁ = 1 - 0.327787
cosθ₁ = 0.672213
θ₁ = cos⁻¹ (0.672213)
θ₁ = 47.76⁰
Thus, the initial angle between the dipole moment and the magnetic field is 47.76⁰