Question

A battery with an emf of 12.0 V shows a terminal voltage of 11.7 V when operating in a circuit with two lightbulbs, each rated at 4.0 W (at 12.0 V), which are connected in parallel.

What is the battery's internal resistance?

Answer 1

`R_i_n_t=0.45 \Omega`

Step-by-step explanation:

Internal resistance is a concept that helps model the electrical consequences of the complex chemical reactions that occur within a battery. When a charge is applied to a battery, the internal resistance can be calculated using the following equation:

`R_i_n_t=((V_N_L)/(V_F_L) -1)R_L`

Where:

`V_F_L=Load\hspace{3}voltage=11.7V\\V_N_L= O pen\hspace{3}circuit\hspace{3}voltage=12V\\R_L=Load\hspace{3}resistance`

As you can see, we don't know the exactly value of the
`R_L`. However we can calculated that value using the next simple operations:

The problem tell us that the power of each lightbulb is 4.0 W at 12.0 V, hence let's calculated the power at 11.7V using Cross-multiplication:

`(12)/(11.7) =(4)/(P)`

Solving for
`P` :

`P=(11.7*4)/(12) =3.9W`

Now, the electric power is given by:

`P=(V^2)/(R_b)`

Where:

`R_b=Resistance\hspace{3}of\hspace{3}each\hspace{3}lightbulb`

So:

`R_b=(V^2)/(P) =(11.7^2)/(3.9) =35.1\Omega`

Now, because of the lightbulbs are connected in parallel the equivalent resistance is given by:

`(1)/(R_L) =(1)/(R_b) +(1)/(R_b) =(2)/(R_b) \\\\ R_L= (R_b)/(2) =(35.1)/(2)=17.55\Omega`

Finally, now we have all the data, let's replace it into the internal resistance equation:

`R_i_n_t=((12)/(11.7) -1)17.55=0.45\Omega`

Answer 2

0.46Ω

Step-by-step explanation:

The electromotive force (E) in the circuit is related to the terminal voltage(V), of the circuit and the internal resistance (r) of the battery as follows;

E = V + Ir --------------------(a)

Where;

I = current flowing through the circuit

But;

V = I x Rₓ ---------------------(b)

Where;

Rₓ = effective or total resistance in the circuit.

First, let's calculate the effective resistance in the circuit:

The effective resistance (Rₓ) in the circuit is the one due to the resistances in the two lightbulbs.

Let;

R₁ = resistance in the first bulb

R₂ = resistance in the second bulb

Since the two bulbs are both rated at 4.0W ( at 12.0V), their resistance values (R₁ and R₂) are the same and will be given by the power formula;

P =
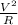
`(V^(2) )/(R)`

=> R =
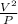`(V^(2) )/(P)` -------------------(ii)

Where;

P = Power of the bulb

V = voltage across the bulb

R = resistance of the bulb

To get R₁, equation (ii) can be written as;

R₁ =
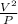`(V^(2) )/(P)` --------------------------------(iii)

Where;

V = 12.0V

P = 4.0W

Substitute these values into equation (iii) as follows;

R₁ =
`(12.0^(2) )/(4)`

R₁ =
`(144)/(4)`

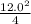
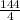
R₁ = 36Ω

Following the same approach, to get R₂, equation (ii) can be written as;

R₂ =
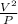`(V^(2) )/(P)` --------------------------------(iv)

Where;

V = 12.0V

P = 4.0W

Substitute these values into equation (iv) as follows;

R₂ =
`(12.0^(2) )/(4)`

R₂ =
`(144)/(4)`

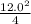
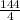
R₂ = 36Ω

Now, since the bulbs are connected in parallel, the effective resistance (Rₓ) is given by;

`(1)/(R_(X) )` =
`(1)/(R_1)` +
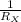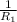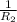`(1)/(R_2)` -----------------(v)

Substitute the values of R₁ and R₂ into equation (v) as follows;

`(1)/(R_X)` =
`(1)/(36)` +
`(1)/(36)`

`(1)/(R_X)` =
`(2)/(36)`

Rₓ =
`(36)/(2)`

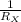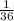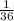
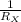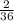
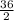
Rₓ = 18Ω

The effective resistance (Rₓ) is therefore, 18Ω

Now calculate the current I, flowing in the circuit:

Substitute the values of V = 11.7V and Rₓ = 18Ω into equation (b) as follows;

11.7 = I x 18

I =
`(11.7)/(18)`

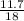
I = 0.65A

Now calculate the battery's internal resistance:

Substitute the values of E = 12.0, V = 11.7V and I = 0.65A into equation (a) as follows;

12.0 = 11.7 + 0.65r

0.65r = 12.0 - 11.7

0.65r = 0.3

r =
`(0.3)/(0.65)`

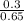
r = 0.46Ω

Therefore, the internal resistance of the battery is 0.46Ω