Question

A toroidal coil has a mean radius of 16 cm and a cross-sectional area of 0.25 cm2; it is wound uniformly with 1000 turns. A second toroidal coil of 750 turns is wound uniformly over the first coil. Ignoring the variation of the magnetic field within a toroid, determine the mutual inductance of the two coils.

Answer 1

Step-by-step explanation:

Mutual inductance is equal to magnetic flux induced in the secondary coli due to unit current in the primary coil .

magnetic field in a torroid B = μ₀ n I , n is number of turns per unit length and I is current .

B = 4π x 10⁻⁷ x (1000 / 2π x .16 )x 1 ( current = 1 A)

flux in the secondary coil

= B x area of face of coil x no of turns of secondary

= 4π x 10⁻⁷ x (1000 /2π x .16 ) .25 x 10⁻⁴ x 750

= 2 x 1000 x .25 x( 750 /.16) x 10⁻¹¹

2343.75 x 10⁻⁸

= 23.43 x 0⁻⁶ H.

.

Answer 2

2.5 x 10^-5 henry

Step-by-step explanation:

The mutual inductance between the toroids is same.

mean radius of the toroid, r = 16 cm = 0.16 m

Area of crossection, A = 0.25 cm²

Number of turns in the first toroid, N1 = 1000

Number of turns in the second toroid, N2 = 750

The formula for the mutual inductance is given by

`M =(\mu_(0)N_(1)N_(2)A)/(l)`

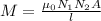
Where, l is the length

l = 2 x 3.14 x r = 2 x 3.14 x 0.16 = 1.0048 m

`M =(4\pi* 10^(-7)* 1000* 750* 0.25* 10^(-4))/(1.0048)`

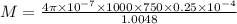
M = 2.5 x 10^-5 henry

Thus, the mutual inductance between the two toroid is 2.5 x 10^-5 henry.