Answer:
2.5 x 10^-5 henry
Step-by-step explanation:
The mutual inductance between the toroids is same.
mean radius of the toroid, r = 16 cm = 0.16 m
Area of crossection, A = 0.25 cm²
Number of turns in the first toroid, N1 = 1000
Number of turns in the second toroid, N2 = 750
The formula for the mutual inductance is given by
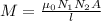
Where, l is the length
l = 2 x 3.14 x r = 2 x 3.14 x 0.16 = 1.0048 m
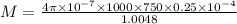
M = 2.5 x 10^-5 henry
Thus, the mutual inductance between the two toroid is 2.5 x 10^-5 henry.