Question

According to the manufacturer of a backup UPS device, the normal output voltage is 120 volts. The sample of 40 measured voltage amounts from a unit have a mean of 123.59 volts and a standard deviation of 0.31 volts. Use a 0.05 significance level to test the claim that the sample is from a population with a mean equal to 120 volts.

Answer 1

Answer: REJECT the null hypothesis; there IS sufficient evidence to warrant a rejection of the claim that the mean voltage is 120 volts.

t-calculated = 73.242

t-critical = 2.023

Answer 2

z = 1.83<1.96

null hypothesis is accepted

The sample is came from a population mean

Explanation:

Step :-1

The sample of 40 measured voltage amounts from a unit have a mean of 123.59 volts and a standard deviation of 0.31 volts

given sample size n =40

mean of the sample ×⁻ = 123.59 volts

standard deviation of sample σ = 0.31 volts

Step2:-

Null hypothesis :-

the sample is from a population with a mean equal to 120 volts.

H₀ : μ =120

Alternative hypothesis:-

H₁ : μ ≠120

level of significance:- α =0.05

Step 3:-

The test statistic

`z = (x_(-)-mean )/((S.D)/(√(n) ) )`

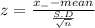
substitute values and simplification

`z = (123.59-120)/((0.31)/(√(40) ) )`

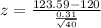
on simplification we get the calculated value

z = 1.83

The tabulated value z =1.96 at 0.05 % level of significance

Conclusion:-

Calculated Z < The tabulated value z =1.96 at 0.05 % level of significance

so the null hypothesis is accepted

The sample is came from a population mean